Deze theorie is uitgewerkt door Allen Forte, op basis van eerder werk van o.a. Georg Perle en Milton Babbitt.
Met deze theorie hebben we een stukje gereedschap in handen om op zoek te gaan naar toonhoogteverbanden in muziek die zich onttrekt aan tonale/modale (harmonische) analyse. Het gaat daarbij niet alleen om identificeren van toongroepen of pitch-class sets (zoals we gewend zijn te doen met een akkoordsymbool zoals G7, Dm, etc.), maar ook om verbanden te leggen tussen die toongroepen (zoals we gewend zijn te doen met harmonische functies en toonsoortrelaties).
In het laatste geval verbinden we bijvoorbeeld het akkoord Gm7 aan een trap in een toonsoort (II 7 in F) en een harmonische functie (Subdominant). We zullen zien dat in niet-tonale/modale muziek er ook verbanden kunnen worden gelegd tussen toongroepen.
Pitch-classes
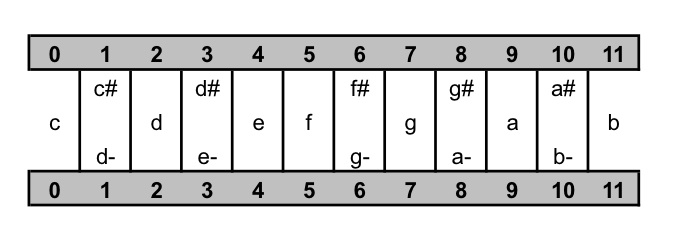
De pitch-class 0 staat voor alle mogelijke c’s, de pitch-class 2 voor alle mogelijke d’s, enzovoort.
Pitch-class 1 staat voor cis of des onafhankelijk in welk octaaf.
Ook traditionele groepen van tonen (bijvoorbeeld akkoorden) kunnen gemakkelijk worden weergegeven.
[0, 3, 7] is een kleine drieklank op c.
[1, 5, 8, 11] een dominantseptiemakkoord op des of cis.
[3, 7, 11] een overmatige drieklank op es of dis.
Uitgaande van 12 pitch-classes is het aantal mogelijke combinaties van tonen eindig.
Cardinal Number
Namen van Pitch-Class Sets bestaan uit twee delen gescheiden door een koppelteken, bijvoorbeeld 3-11 of 4-27.
Het eerste cijfer of getal geeft het aantal pitch-classes aan, dit is het zogenaamde cardinal number. Het tweede is het getal van de plaats in de lijst van pitch-class sets met dat betreffende aantal pitch-classes.
Normal order
Gerangschikt van “laag” naar “hoog”.
Best Normal Order
De meest compacte vorm gerangschikt van “laag” naar “hoog”
Prime Form
De meest compacte vorm met de kleinste intervallen aan de basis.
Als de omkering van deze compacte vorm nog kleinere intervallen aan de basis oplevert, wordt deze gekozen.
Dit is de Prime Form. Alle Prime Forms in de lijst zijn getransponeerd naar pitch-class 0. (vergelijkbaar met cheat-sheets voor codering van akkoordsymbolen zoals Aebersold bijvoorbeeld).
Intervallen en Interval Class
Complementaire intervallen worden gezien als één interval class: dus een grote sekonde (2) en zijn omkering, een kleine septiem (10) worden gezien als vertegenwoordiger van één interval-class, namelijk 2. We noemen ze elkaars equivalent.
Interval Vector
Aanvaarden we het principe van equivalentie, dan volgt daaruit dat er strikt genomen 6 interval-classes overblijven:
na 6 halve toonsafstanden (3 hele toonsafstanden), een tritonus dus(!) volgt de reine kwint die een omkering is van de kwart.
Deze 6 interval-classes worden gebruikt om mogelijke interval-class combinaties aan te geven van een pitch-class set, de Interval Vector, geplaatst tussen < >.
De interval vector bestaat uit 6 cijfers op 6 “posities”, bijvoorbeeld <002001> behorend bij pc-set 3-11, die we kennen als de verminderde drieklank:
- positie 1: kleine sekonde: 0 maal mogelijk
- positie 2: grote sekonde: 0 maal mogelijk
- positie 3: kleine terts: 2 maal mogelijk
- positie 4: grote terts: 0 maal mogelijk
- positie 5: reine kwart; 0 maal mogelijk
- positie 6: tritonus: 1 maal mogelijk.